Dijkstra Algorithm 02 (Procdure)
다익스트라 알고리즘의 개념 설명에 이어, 이번 포스트에서는 알고리즘의 자세한 진행 과정에 대해 정리한다.
알고리즘 구현 방법
대표적인 다익스트라 알고리즘의 구현 방법은 우선순위 큐(priority queue)를 사용한 너비 우선 탐색(breadth first search)이다. 너비 우선 탐색으로 그래프의 각 노드를 방문해가며, 중요한 방문 순서는 우선순위 큐에 의해서 결정된다. 너비 우선 탐색은 우선순위 큐가 아닌 일반적인 큐를 사용할 때의 탐색 방식이므로, 사실 너비 우선 탐색이 아닌 최단거리 우선 탐색이 더 정확한 표현이 되겠다.
우선순위 큐는 저장된 요소들 중 최소(혹은 최대)값을 항상 큐의 top 위치로 정렬해주는 데이터 구조다. 따라서 큐의 top 에서 값을 꺼내면 항상 최소(최대)값을 얻는다. top 을 제외한 다른 요소들은 정렬되어있지 않는 대신, 정렬 과정이 빠르다. 우선순위 큐는 이진 트리 (binary tree)로 구현할 수 있지만, 제공되는 라이브러리를 쓰는 것이 아무래도 편리하다.
우선순위 큐에는 어떤 값이 들어가야할까? 어느 노드에 먼저 방문해야하는지, 즉 어느 노드가 최단거리 노드인지를 확인할 수 있는 값이 필요하다. 따라서 노드의 번호와 해당 노드까지의 거리가 쌍(pair)으로 묶여서 저장되어야한다. 우선순위 큐는 요소의 거리값을 기준으로 최소값을 가진 요소를 top으로 보내주도록 설정하면 된다.
시적점으로부터 각 노드까지의 최단거리를 저장할 결과 배열(output array)과, 이미 방문한 노드를 재방문하지 않도록 체크해주는 방문 배열도 필요하다. 방문 배열은 사실 꼭 필요하진 않지만 (어차피 재방문했을 경우엔 최단거리보다 더 큰 거리가 나올 것이므로), 불필요한 탐색 속도를 줄여준다.
알고리즘 예제
예시 그래프를 통해 다익스트라 알고리즘을 실제로 파악해보자.
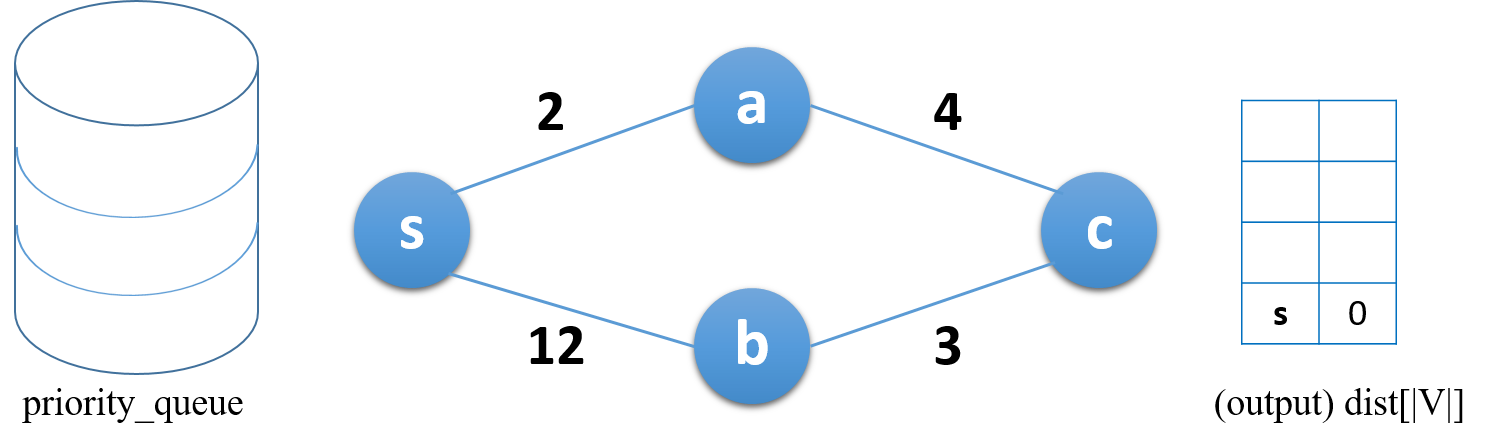 그래프와 우선순위 큐, 결과를 저장할 행렬을 준비한다.
그래프와 우선순위 큐, 결과를 저장할 행렬을 준비한다.
방문여부 행렬 초기화(모든 값이 false), 결과행렬 초기화(모든 값이 infinite)
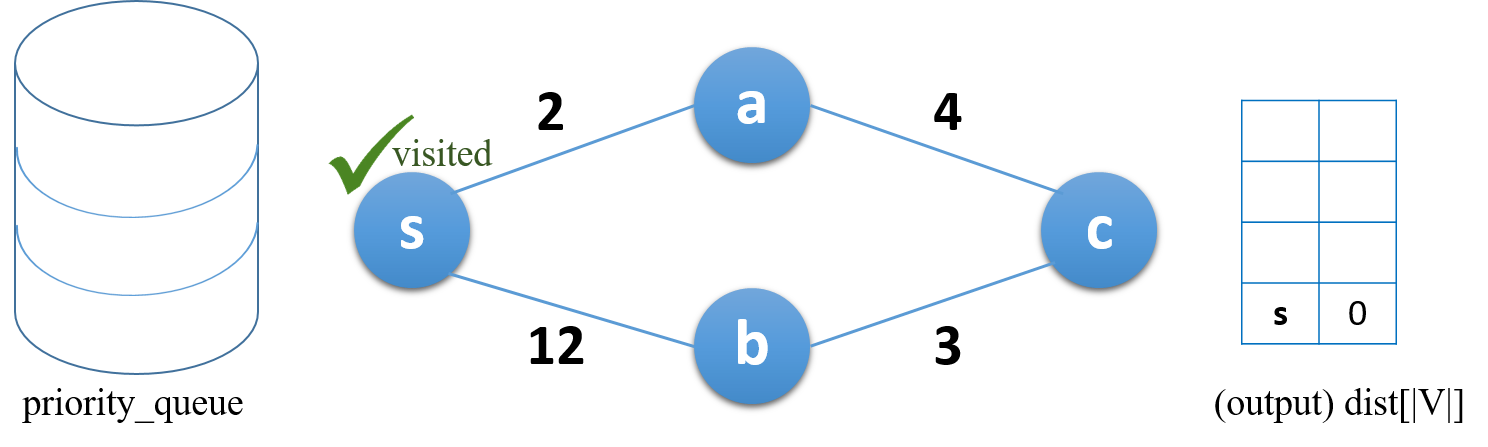 노드 s 에서부터 시작 (시작점에서 시작점까지의 거리는 0)
노드 s 에서부터 시작 (시작점에서 시작점까지의 거리는 0)
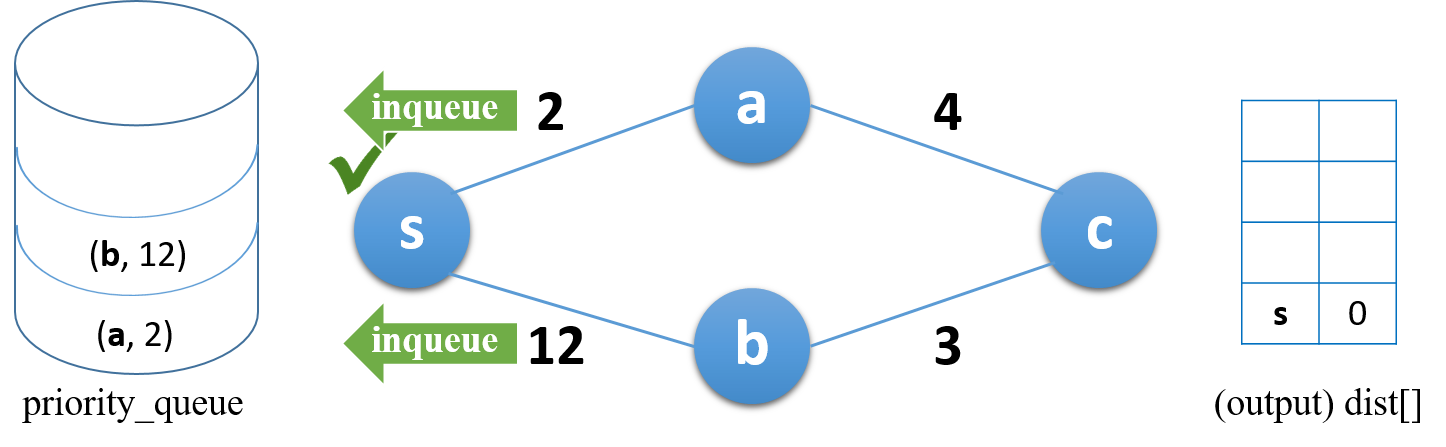 연결된 모든 인접 노드(a, b)를 큐에 추가
연결된 모든 인접 노드(a, b)를 큐에 추가
가장 작은 거리를 가진 항목이 top 으로 이동
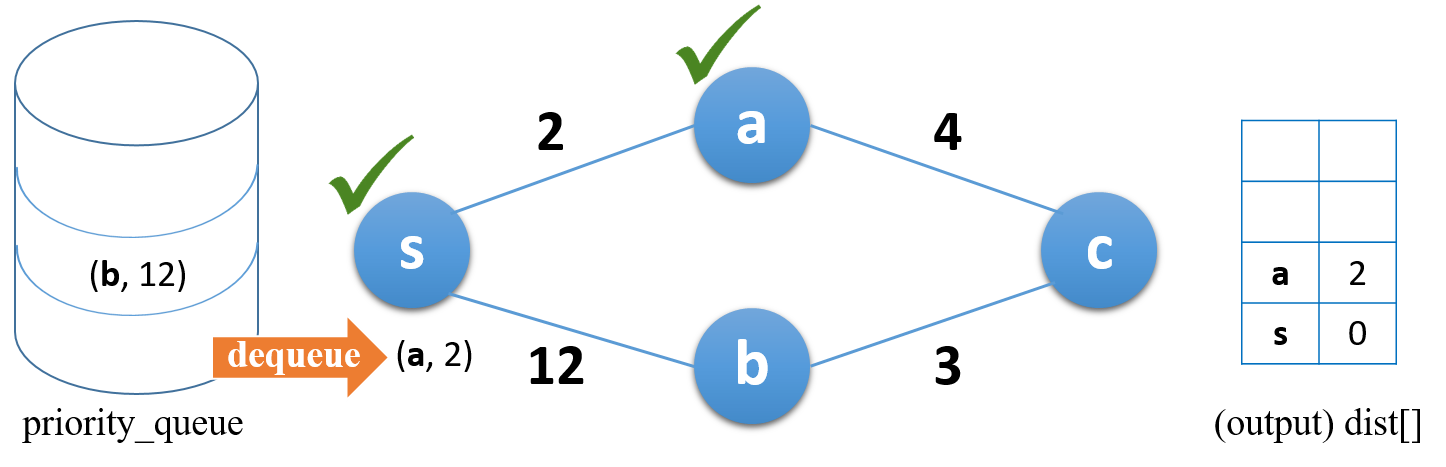 큐에서 top 값 (a, 2)을 빼냄과 동시에 해당 노드를 방문
큐에서 top 값 (a, 2)을 빼냄과 동시에 해당 노드를 방문
빠진 거리값(2)이 해당 노드까지의 최단거리이므로, 이를 결과 행렬에 저장
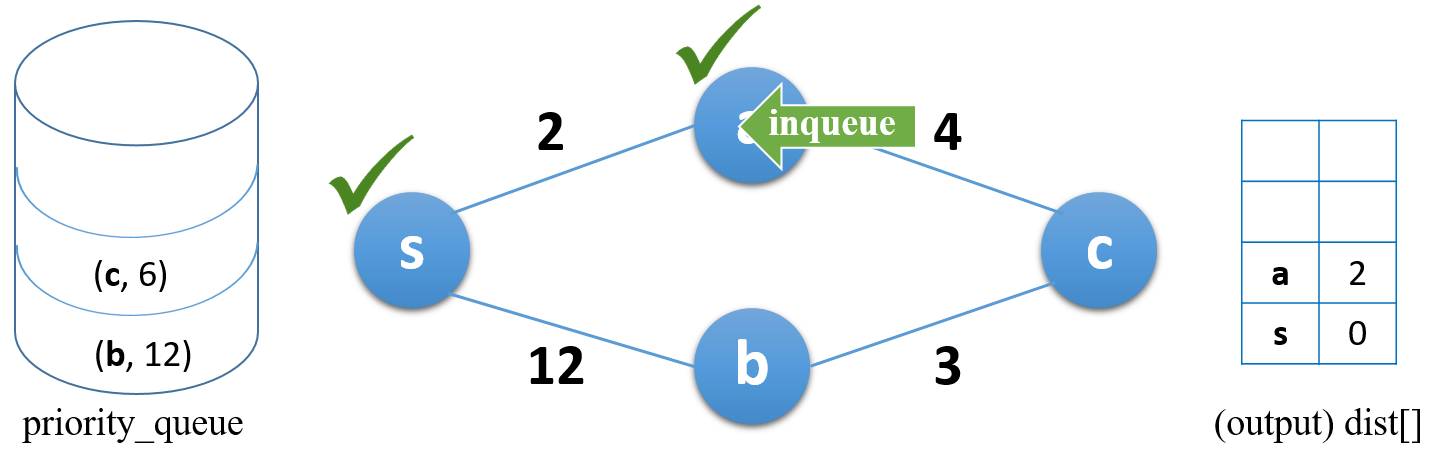 두 번째로 방문한 노드(a)에서 같은 동작을 수행
두 번째로 방문한 노드(a)에서 같은 동작을 수행
인접 노드(c)를 큐에 추가 (이미 방문한 노드(s)는 다시 갈 필요 없으므로 제외)
현재 노드까지의 최단거리(2)와 현재 노즈에서 인접 노드까지의 거리(4)를 더한 값(6)이 인접 노드까지의 총 거리가 되므로, queue에는 (c, 6)이 입력됨
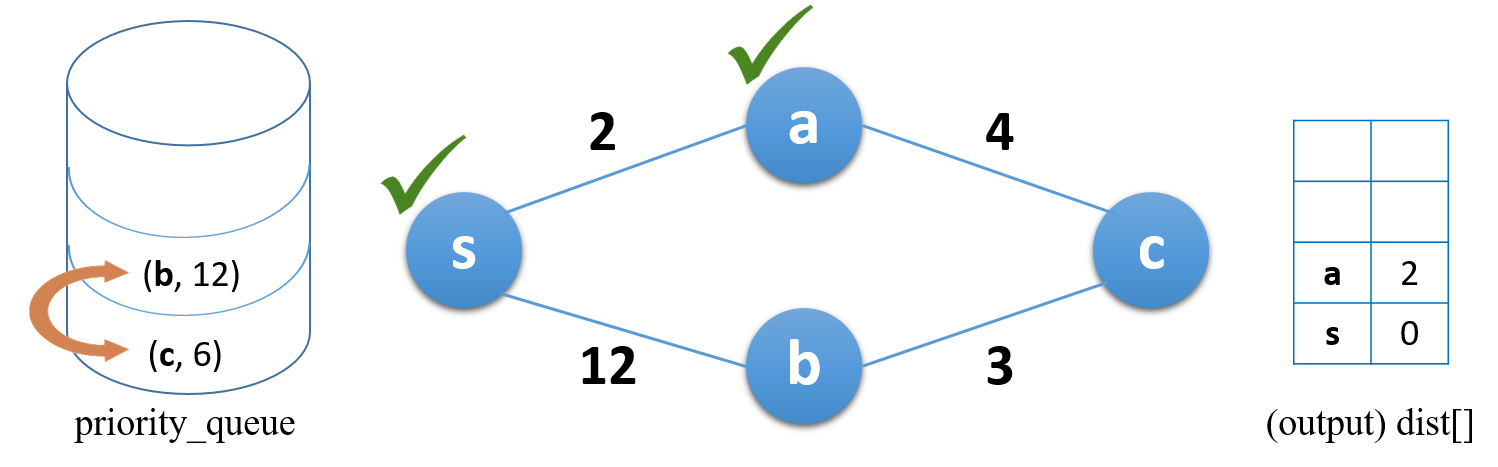 우선순위 큐에 의해 추가된 항목 중 가장 작은 거리를 갖는 노드가 top 으로 이동
우선순위 큐에 의해 추가된 항목 중 가장 작은 거리를 갖는 노드가 top 으로 이동
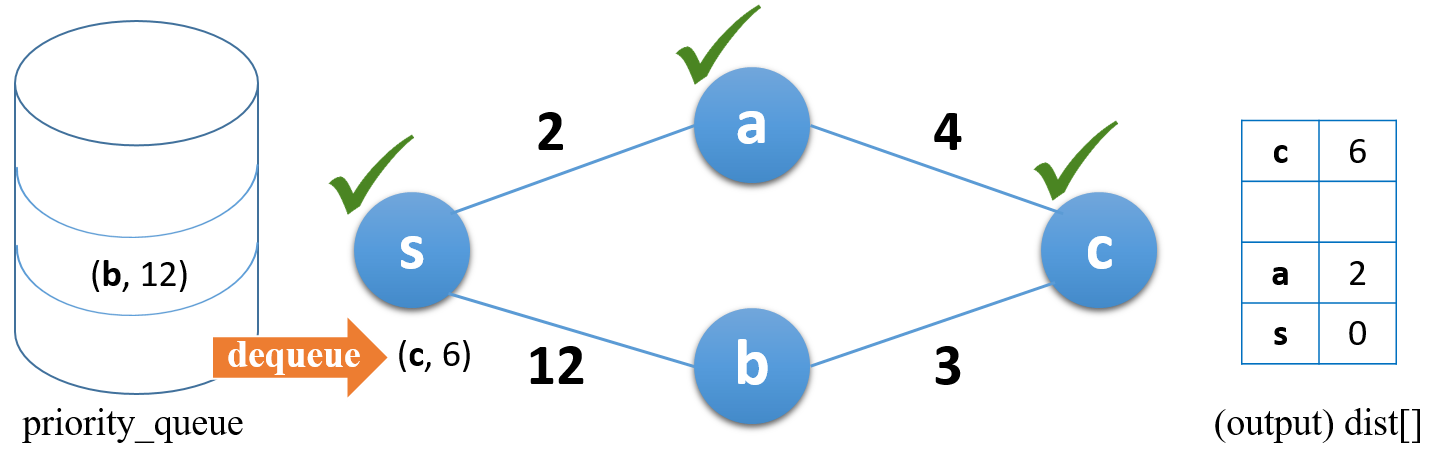 큐에서 top 항목을 꺼내며 꺼낸 노드(c)를 방문 (결과 행렬 갱신)
큐에서 top 항목을 꺼내며 꺼낸 노드(c)를 방문 (결과 행렬 갱신)
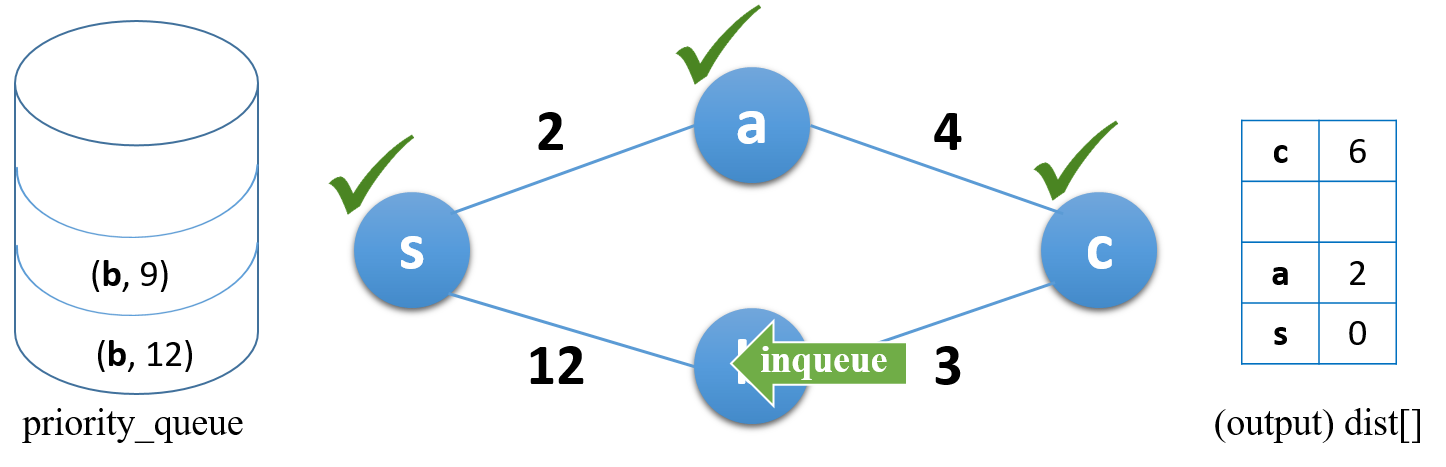 방문한 노드의 인접 노드(b)를 다시 큐에 추가
방문한 노드의 인접 노드(b)를 다시 큐에 추가
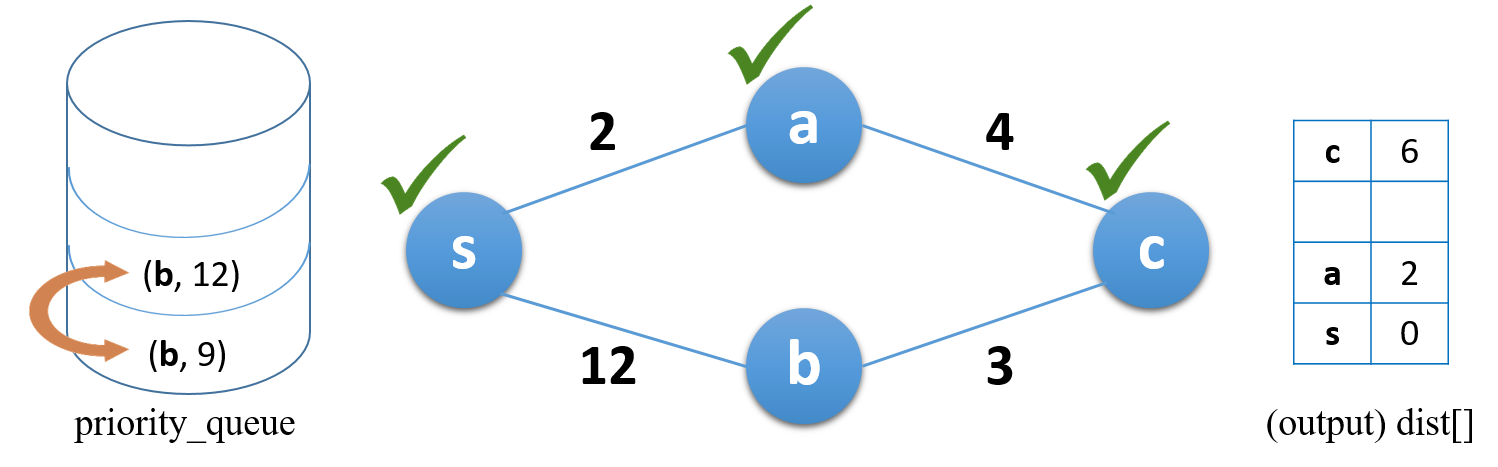 우선순위 큐의 항목들 중 가장 작은 거리를 갖는 노드가 맨 밑으로 온다.
우선순위 큐의 항목들 중 가장 작은 거리를 갖는 노드가 맨 밑으로 온다.
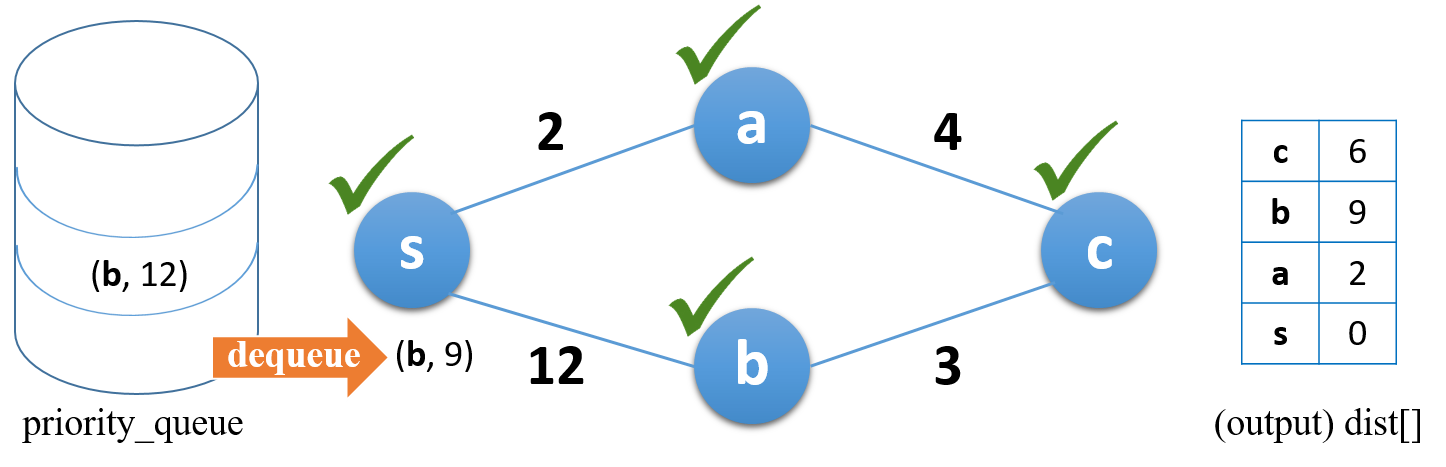 큐에서 값을 꺼내며 방문 (결과 행렬 갱신)
큐에서 값을 꺼내며 방문 (결과 행렬 갱신)
(b, 12)가 큐에 먼저 입력되었지만, 우선순위 큐에 의해 더 거리가 가까운 (b, 9)가 먼저 꺼내어지는 것을 확인할 수 있다.
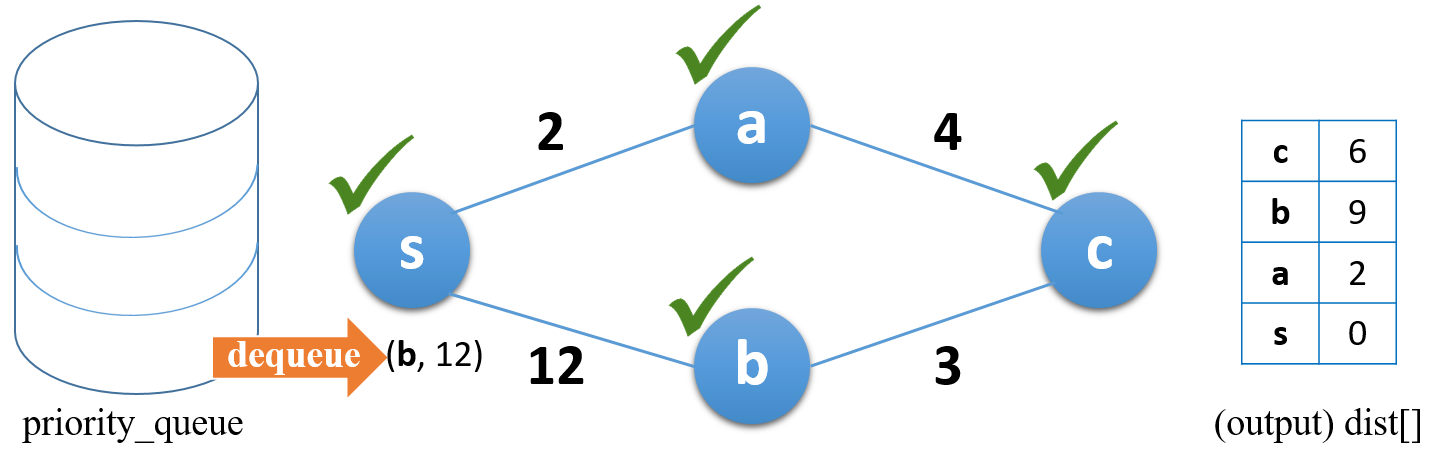 우선순위 큐의 top에 있는 (b, 12) 를 꺼낸다. 이미 방문했으므로 skip. 우선순위 큐가 empty 상태가 되면 알고리즘이 종료된다.
우선순위 큐의 top에 있는 (b, 12) 를 꺼낸다. 이미 방문했으므로 skip. 우선순위 큐가 empty 상태가 되면 알고리즘이 종료된다.
코드
VS2015 에서 작성하였다.#include <iostream>
#include <queue>
#include <vector>
#include <functional> // std::greater
#include <utility> // pair
using namespace std;
typedef vector<vector<int>> array2d;
typedef pair<int, int> pos2d;
void Dijkstra(array2d& input, array2d& dist, const int h, const int w)
{
// priority queue
priority_queue<int, vector<pair<int, pos2d>>, greater<pair<int, pos2d>>> q; // sort the smallest element at the top
// Initialization (start node)
q.push(pair<int, pos2d>(0, pos2d(0, 0))); // push starting node
dist[0][0] = 0; // update distance
// Loop
while (!q.empty())
{
pair<int, pos2d> e = q.top(); // pop element with the smallest distance
q.pop();
int here_x = e.second.first;
int here_y = e.second.second;
int here_min_dist = dist[here_y][here_x];
int here_dist = e.first;
// path with smaller dist. already exists
if (here_min_dist < here_dist) // equal is missing because of the first iteration
continue; // skip the node
vector<vector<int>> delta;
delta.push_back(vector<int>({ 0, -1 })); // top
delta.push_back(vector<int>({ -1, 0 })); // left
delta.push_back(vector<int>({ 1, 0 })); // right
delta.push_back(vector<int>({ 0, 1 })); // dowm
for (auto d : delta)
{
int there_x = here_x + d[0];
int there_y = here_y + d[1];
// out of index
if (there_y < 0 || there_y >= h || there_x < 0 || there_x >= w)
continue;
int there_min_dist = dist[there_y][there_x];
int there_dist = here_min_dist + input[there_y][there_x];
// if path with smaller dist is found
if (there_dist < there_min_dist)
{
cout << "(" << there_x << ", " << there_y << ")" << endl;
// push neighbor node, update distance
q.push(pair<int, pos2d>(there_dist, pos2d(there_x, there_y)));
dist[there_y][there_x] = there_dist;
}
}
}
}
void main()
{
// Input: 2D matrix
const int height = 4;
const int width = 3;
array2d input;
input.push_back(vector<int>({ 0, 1, 1 }));
input.push_back(vector<int>({ 1, 1, 1 }));
input.push_back(vector<int>({ 1, 1, 0 }));
input.push_back(vector<int>({ 1, 1, 0 }));
// Output: array for minimum distance
array2d dist;
dist.push_back(vector<int>({ INT_MAX, INT_MAX, INT_MAX }));
dist.push_back(vector<int>({ INT_MAX, INT_MAX, INT_MAX }));
dist.push_back(vector<int>({ INT_MAX, INT_MAX, INT_MAX }));
dist.push_back(vector<int>({ INT_MAX, INT_MAX, INT_MAX }));
// Run algorithm
Dijkstra(input, dist, height, width);
// Print output
for (int y = 0; y < height; y++)
{
for (int x = 0; x < width; x++)
cout << dist[y][x] << ", ";
cout << endl;
}
// Pause
char a;
cin >> a;
}
QnA
Q) 우선순위 큐를 쓰는 이유?
A) 최단거리 노드를 우선적으로 방문하기 위함. 달리 말하면, 더 늦게 ‘발견’한 노드라도 더 먼저 ‘방문’할 수 있게 하기 위함
Q) ‘방문’ 시점은 큐에서 요소를 꺼낼 때인데, 최단거리 정보는 왜 요소를 넣을 때 갱신하나?
A) 코드상의 단순한 트릭. 불필요한 노드는 애초에 큐에 넣지 않음으로써, 큐에서 꺼내고 확인해서 버리는 절차를 줄여 속도가 개선된다.
우선순위 큐를 사용하지 않는 Dijkstra
우선순위 큐를 사용하는 다익스트라 알고리즘은, 너비 우선 탐색을 기본으로 하므로 인접 간선의 갯수만큼 탐색을 시도한다. 따라서 그래프의 간선의 갯수가 노드의 갯수보다 훨씬 많을 경우에는 (방문 횟수는 노드 갯수만큼 하지만) 탐색 횟수가 늘어나 속도가 느려진다. 그럴 때는 좀 더 효율적인 방법이 있다.
핵심 논리는 우선순위 큐를 이용한 다익스트라와 같다. 우선순위 큐가 하는 역할은 결국 현재 노드로부터의 ‘최단거리 인접 노드’를 뱉어주는 것이므로, 매 iteration마다 최단거리 노드를 다른 방식으로 찾으면 된다. 어떻게? 방법은 오히려 더 간단하다. 현재 노드를 제외한 (아직 방문하지 않은) 모든 노드를 full search 하면서 어느 노드가 가장 가까운지 찾고, 최소 거리 노드를 방문하면 된다.
조건
어떤 그래프에서 다익스트라를 사용할 수 있을까?
무방향 그래프의 경우, 모든 간선의 가중치 값이 양수여야만 알고리즘을 적용할 수 있다. 만약 가중치 값에 음수가 존재하면, 다익스트라 알고리즘이 최단거리를 빠르게 찾기 위한 전제조건이 성립되지 않아 적용이 불가능하다. 게다가, 만약 동일한 간선을 여러번 지날 수 없다는 조건이 따로 있지 않다면, 음수 가중치를 갖는 간선을 무한대로 왕복하면 최단거리가 마이너스 무한대가 나올 것이다. 문제 자체가 성립되지 않는다.
방향 그래프의 경우엔, 음수 사이클이 없다면 적용 가능하다. 음수 사이클이란, 무한히 같은 경로를 돌면서 거리가 마이너스 무한대로 발산할 수 있는 경로를 의미한다.
설명의 편의를 위해, 여기서는 모든 간선 가중치 값이 양수인 무방향 그래프를 가정하고 설명을 진행하였다.