Dijkstra Algorithm 01 (Intro)
최단거리 문제
알고리즘 문제를 풀다 보면, “어떤 점수의 최대값, 최소값 등을 구하시오.” 같은 문제를 본다. 이 때 문제가 그래프로 모델링 가능하다면, 대부분 그래프의 최단거리를 계산함으로써 답을 구할 수 있다.
예시 문제: 알고스팟_BFS
그래프(Graph)란?
그래프는 정점(node) 과 간선(edge)으로 이루어진 집합을 의미한다. 각 간선은 가중치(weight)를 가지고 있을 수 있으며, 가중치가 없을 때는 모든 간선이 1 의 가중치 값을 갖는다고 가정한다.
또한, 간선의 방향성에 따라 간선에 방향성이 있으면 방향 그래프(directed graph), 방향성이 없으면 (양 방향으로 이동이 가능) 무방향 그래프(undirected graph)로 분류된다.
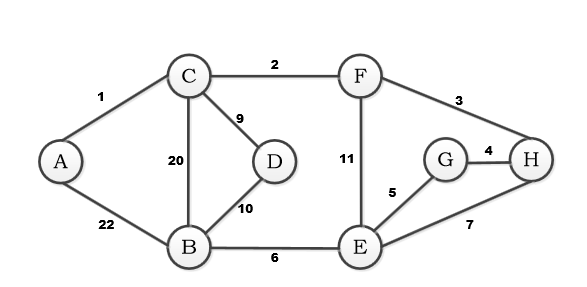
undirected graph with weighted edges
그래프의 경로(path)와 거리(distance)
그래프의 한 정점으로부터 다른 정점으로 이동하기 위해 지나는 간선들의 집합을 그래프의 경로(path)라고 한다. 이 때, 경로의 가중치 값을 모두 더한 값이 그 경로의 거리(distance)이다.
그래프의 최단거리란, 특정 시작 정점 s에서 출발하여 종료 정점으로 도착하기까지 지나는 모든 경로 중에서 가장 거리가 작은 경로의 거리 값을 의미한다.
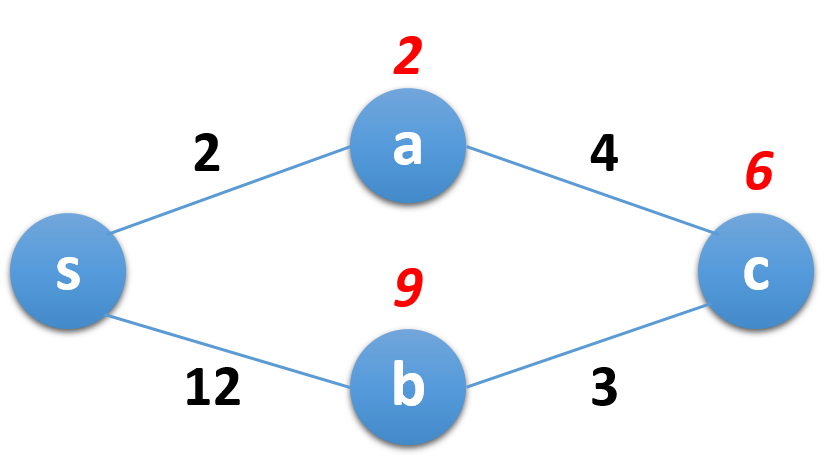
minimum distances (red figures) from s to each node.
그래프의 최단거리를 구하는 알고리즘은 여러 가지가 존재하지만, 이 포스트에서는 그 중 가장 유명한(?) 다익스트라(Dijkstra) 알고리즘에 대해 공부한 내용을 정리해본다.
다익스트라(Dijkstra) 알고리즘
목적
다익스트라 알고리즘은 정해진 시작 정점 s로부터 다른 모든 정점까지의 최단거리를 구해주는 알고리즘이다.
그래서 시작점이 정해져 있는 문제에서 사용되며, 시작점이 정해져있지 않을 때는 다익스트라를 여러 번 실행해야 한다.
개념
최단거리를 어떻게 구해야할까? 일단, 그래프의 노드를 방문하는 탐색(traverse)을 수행해야한다. 너비 우선 탐색(breadth first search)이나 깊이 우선 탐색(depth first search)같은 탐색 방법에 대한 자세한 설명은 생략하겠다. 그리고, 탐색을 통해 노드를 방문할 때마다 그 노드까지의 거리를 저장할 수 있는 버퍼도 필요하다. 그렇다면, 노드를 방문하면서 시작점으로부터의 거리를 버퍼에 기록해나가면 최단 거리를 구할 수 있을까?
단순한 사고는 여기에서 문제점에 봉착한다. 임의의 탐색을 통해 노드를 방문하며 거리를 저장한다한들, 그 거리가 최단거리임을 어떻게 보장할 수 있을까? 아주 많은 횟수만큼 반복 방문을 수행하며 더 이상 거리가 더 작아지지 않을 때까지 탐색을 계속해야한다. 더구나, 탐색을 무한히 반복하지 않는 이상, 지금까지 구해놓은 각 노드까지의 거리가 해당 노드까지의 최단거리임을 확신할 수 없을 것이다.
다익스트라 알고리즘은, 이런 문제점을 해결하기 위해 greedy 한 접근법을 통해 최단거리를 찾는다. 즉, “현 시점에서 최단거리임을 확신할 수 있는” 노드를 우선적으로 방문하여 결과 버퍼를 채워나가며, 모든 노드를 각 한 번 씩만 방문하고도 모든 노드의 최단거리를 구할 수 있는 알고리즘이다.
그렇다면 어떤 노드가 최단거리임을 확신할 수 있는 노드일까? 무조건 이보다 더 짧은 거리는 없다고 확신할 수 있는 노드는 무엇일까? 여기에 약간의 사고가 필요하다.
현재 노드에 간선으로 연결되어 있는 노드를 인접 노드(adjacent node)라 부른다. 인접 노드로 연결된 간선에는 저마다 가중치 값이 있고, 모든 가중치 값은 양수라고 가정해보자. 그렇다면 인접 간선 중 가장 작은 가중치 값을 갖는 간선은 최단거리를 만드는 경로라고 말할 수 있다. 예를 들어, 노드 s로부터 3 개의 간선이 다른 노드 a, b, c와 연결되어있고, 각 간선의 가중치 값이 1, 2, 3 이라고 할 때, s에서 a로 향하는 최단거리는 가장 작은 가중치 값인 1이 된다. 왜냐하면, 만약 a가 아닌 b나 c를 통해 a까지 가는 더 작은 거리가 있다고 한다면, 이는 1보다 더 작아야 한다. 그러나 이미 b나 c로 이동하는 순간 1 보다 거리가 커지며, 이후 어느 간선을 경유한다고 해도 음수 가중치는 없다고 전제하였으므로 거리는 1보다 작아질 수 없다. 따라서 인접한 간선 중 가장 작은 가중치 값을 가진 간선은 최단거리를 이루는 간선이라고 확신할 수 있다. 그러한 간선을 갖는 노드만 우선적으로 방문한다면, 노드 갯수에 비례하는 복잡도 내에서 최단거리를 계산할 수 있게 된다.
위의 greedy 개념을 이용하여 계산하는 것이 다익스트라 알고리즘이며, 많이들 사용되는 방법론을 다음 포스트에서 설명하도록 하겠다.